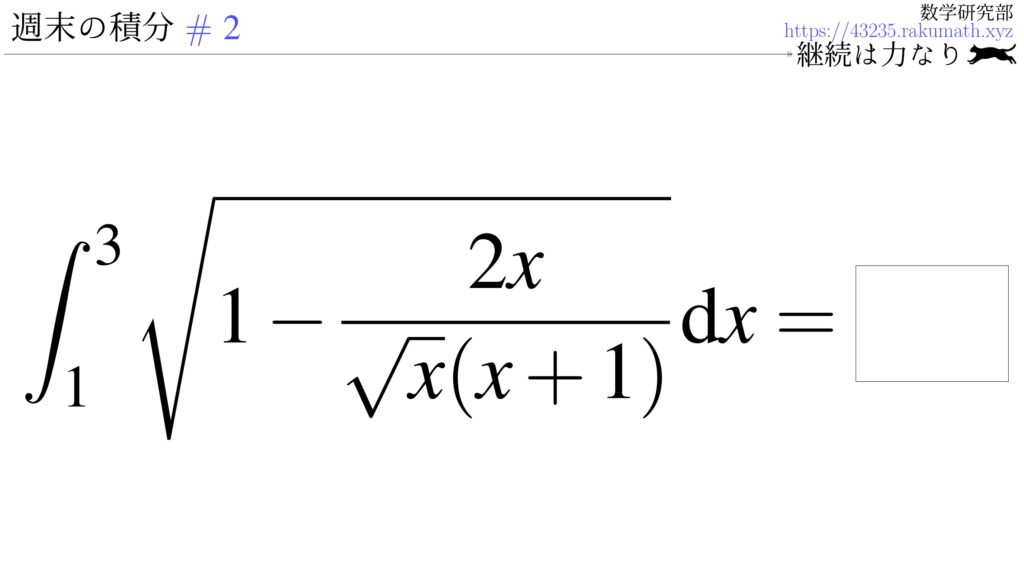週末の積分 #1

この記事は先日公開した「週末の積分 #0」に掲載されていた問題の解説です。

前回の解説

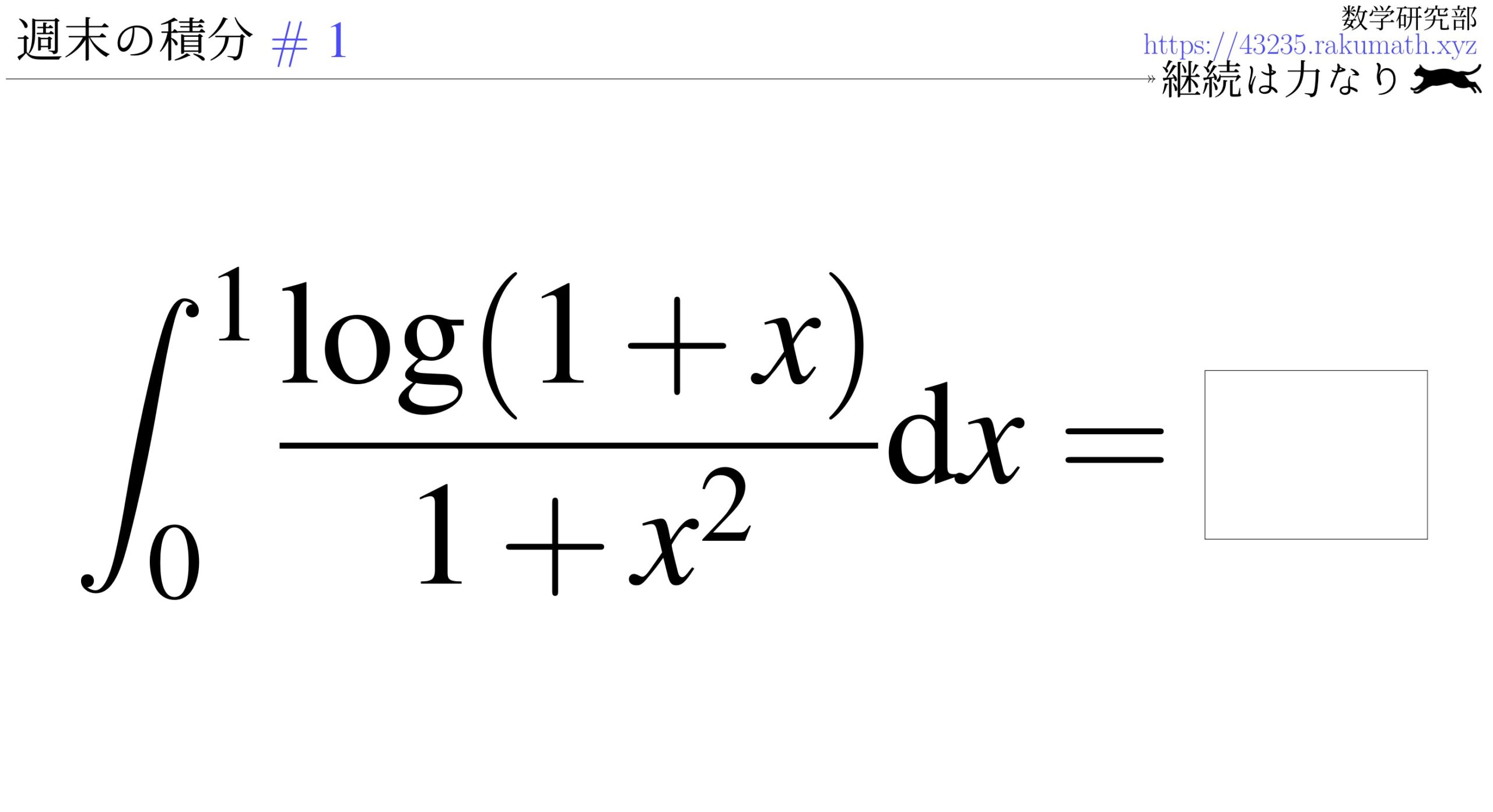
Point:被積分関数に$x^2+a^2$ の形が含まれていれば $x=a\tan{\theta}$ の置換を行う。

今回は$a^2$の部分が1なので、$x=\tan\theta$の置換を行います。
これは補足ですが、”三角関数は二乗に強い”ので、将来的には「$x^2-\,$」と見たら$\sin$置換か$\cos$置換とも思いつくようになりましょう(恐らく日本の学習指導要領ではこちらを先に学習しますが…)。それでは答案です。

与式において$x=\tan\theta$の置換を行うと、
\begin{split}
\text{(与式)}&=\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\frac{\log(1+\tan\theta)}{1+\tan^2\theta}(\tan\theta)^{\prime}\ \mathrm{d}\theta \\&=\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\frac{\log(1+\tan\theta)}{1+\tan^2\theta}\cdot\frac{1}{\cos^2\theta}\ \mathrm{d}\theta \\&=\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\frac{\log(1+\tan\theta)}{\cos^2\theta+\tan^2\theta\cos^2\theta}\ \mathrm{d}\theta \\&=\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\frac{\log(1+\tan\theta)}{\cos^2\theta+\sin^2\theta}\ \mathrm{d}\theta \\&=\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\log(1+\tan\theta)\ \mathrm{d}\theta(=\mathrm{I}_{1}) \end{split}

この後は主に① $\log$ の中身を丁寧に分解していく方法と、② King Property を用いて $\tan$ の加法定理から求める方法の二つがあります。

① $\log$ の中身を丁寧に分解していく方法

$$\begin{split}
\mathrm{I}_{1}&=\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\log\left(1+\frac{\sin\theta}{\cos\theta}\right)\ \mathrm{d}\theta\\&=\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\log\left(\frac{\cos\theta+\sin\theta}{\cos\theta}\right)\ \mathrm{d}\theta\\&=\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\log\left(\frac{\sqrt{2}\cos\left(\theta-\dfrac{\lower.44ex\hbox{$\,\pi\rule{0pt}{1.5ex}\,$}}{\lower-.1ex\hbox{$\,4\,$}}\right)}{\cos\theta}\right)\ \mathrm{d}\theta\\&=\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\log\sqrt{2}\ \mathrm{d}\theta+\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\log\left\{\cos\left(\theta-\frac{\pi}{4}\right)\right\}\ \mathrm{d}\theta-\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\log(\cos\theta)\ \mathrm{d}\theta\\&=\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\log\sqrt{2}\ \mathrm{d}\theta+\displaystyle\int_{-\normalsize\mbox{$\frac{\pi}{4}$}}^{0}\log(\cos\theta)\ \mathrm{d}\theta-\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\log(\cos\theta)\mathrm{d}\theta
\end{split}

最終行の式変形はKing Propertyの考え方を使っています。

\begin{split}
\text{(続き)}&=\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\log\sqrt{2}\ \mathrm{d}\theta+
\displaystyle\int_{-\normalsize\mbox{$\frac{\pi}{4}$}}^{\normalsize\mbox{$\frac{\pi}{4}$}}\log(\cos\theta)\ \mathrm{d}\theta-2\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\log(\cos\theta)\ \mathrm{d}\theta\\&=\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\log\sqrt{2}\ \mathrm{d}\theta+2\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\log(\cos\theta)\ \mathrm{d}\theta-2\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\log(\cos\theta)\ \mathrm{d}\theta\\&=\displaystyle\int_{0}^{\normalsize\mbox{$\frac{\pi}{4}$}}\log\sqrt{2}\ \mathrm{d}\theta=\biggl[\theta\log\sqrt{2}\biggr]^{\normalsize\mbox{$\frac{\pi}{4}$}}_{0}=\frac{\pi}{4}\log\sqrt{2}=\textcolor{red}{\frac{\pi}{8}\log2}
\end{split}